[CRDT] LSEQ: 분산 협업 편집에서 시퀀스를 위한 적응적 구조 번역

원문 링크

 

1. 소개

이 논문에서는 선, 단어, 문자와 같은 기본 요소의 순서를 구현하는 것을 시퀀스 CRDT라고 부른다. 시퀀스 CRDT는 삽입 횟수에 따라 선형적인 공간복잡도를 갖는다. 따라서 편집 동작에 크게 의존한다. 일부 편집 시나리오는 영구적인 성능 저하로 이어지기도 한다. 요소의 전체 순서를 유지하기 위해 구조의 각 기본 요소(문서편집기에서는 문자)에 고유하고 변경 불가능한 식별자가 할당된다. 식별자도 종류가 있는데...

1. 고정 크기 식별자 
   • 예: WOOT, CT, RGA 등.
   • 툼스톤이 있기 때문에 주기적으로 정리하는 고비용 연산 필요.
   • 식별자 길이가 고정이니까 식별자 자체 크기는 일정하게 유지됨.
   • 하지만 삭제 연산이 많이 발생하면 툼스톤 수가 증가하여 공간 복잡도가 높아짐.
2. 가변 크기 식별자 
   • 예: Logoot
   • 툼스톤이 필요하진 않지만 식별자가 무한대로 커질 수 있음. 
   • 삽입 연산이 많이 발생하면 식별자 크기가 증가하여 공간 복잡도가 높아짐.

두 방식 모두 삽입, 삭제 연산의 수에 따라 선형적인 공간 복잡도를 갖는다.

예를 들어 고정 크기 식별자의 경우, 100만개의 연산 이후 단 하나의 줄만 남아있더라도 499,999개의 툼스톤이 존재하는 최악의 시나리오도 가능하다. 반면 가변 크기 식별자의 경우에는 단 하나의 요소의 길이가 499,999인 식별자를 가질 수 있다. 

이러한 문제를 해결하기 위해 Treedoc은 툼스톤과 가변 크기 식별자 모두 사용하지만 식별자가 너무 커질 때 복잡한 가비지 컬렉션 프로토콜에 의존한다. 

 

이 논문에서는 가변 크기 식별자의 시퀀스 CRDT에 속하는 LSEQ라는 새 접근 방식을 제안한다. 최신 기술과 비교했을 때 LSEQ는 공간 복잡성에서.. 뭐라는겨. 암튼 기존보다 뛰어나다네요.

 

2. 서론

식별자를 가능한한 작게 유지하는게 목표고, 리밸런싱하는 비용을 줄일 것이다. 

정의1은 문서를 $(elt,id)$ 쌍 집합으로 본다. $elt$는 문자나 그런 거고. $id$는 고유 불변 식별자인데, 모든 가능한 식별자들 $L$의 집합에 정의되어 있다. $L$은 순서 관계를 갖는데, <는 엄격하게 완전하게 정렬된 순서 관계를 갖는다. 예를 들어, 만약 $x,y\in L$이고, $x<y$이면, $\mathrm{\exists }z\in L,z\ne x,z\ne y,x<z<y$ 이다. 풀어서 설명하면, 만약 x와 y가 집합 $L$에 속하고, x가 y보다 작다면, x와 y의 사이에는 항상 x, y와는 다른 수 z가 있다는 뜻이다. 

 

 

*정의1(문서 모델)

문서는 집합 $D=(elt,id)$이고, 두 연산을 갖는다.

• 삽입(p ∈ L, elt, q ∈ L): $D\cup (elt,i{d}_{elt}),i{d}_{elt}=alloc(p,q)단p<i{d}_{elt}<q$
  • p와 q사이의 $i{d}_{elt}$를 특정 $alloc()$으로 할당해서 만들고, $(elt,i{d}_{elt})$와 $D$를 합치는 것이라고 생각하면 되나?
• 삭제 : 뭐라는겨

 

*정의 2 (가변 크기 식별자)

가변 크기 식별자 $id$는 숫자의 순서이며, 트리의 경로로 지정될 수 있다. 

 

각 식별자가 루트에서 리프까지의 경로인 트리로 문서를 표현한다.

• 만약 p = [11], q = [14]면 삽입 연산을 위한 자리가 존재한다. 식별자 [12], [13] 모두 가능한 선택이다. 
• 만약 p = [14], q = [15]면 이 레벨에는 더이상 자리가 없다. 그렇기 때문에 할당 함수 $alloc$으로 새 레벨을 만들고, [14.0]과 [14.99] 사이에서 새 식별자를 선택할 수 있다. 

여기까진 뭐, 이해됨.

 

할당 전략

랜덤과 바운더리 전략이 있는데 랜덤은 성능 안좋다고 하고,

바운더리 전략: 경계가 지정된 두 이웃 식별자 사이의 값 중에서 랜덤으로 선택하면서, 새 식별자를 이전 식별자에 더 가깝게 할당한다. 물론 오른쪽에서 왼쪽으로 편집할 때 더 잘 작동한다고? 그 반대 아닌가.. 

 

*정의3

$D$는 n 삽입 연산이 수행된 문서라고 가정한다. 

$\sum _{id\in L}^N\frac{(lo{g}_2(id))}{n}<O(n)$

아 나도 뭐라는지 모르겠어서 ai 도움을 받았다. 위 식은 이러한 식별자 할당 방식의 공간 복잡도를 나타낸다. 

수식의 의미는, 모든 식별자의 이진 로그의 값을 n으로 나눈 값이 $O(n)$보다 작다는 것을 나타낸다. 

아무튼 O(n)보다 효율 좋다는 것이겠지... 

 

3. LSEQ 할당 함수

두 식별자 p, q 사이에 새 레벨을 생성할 때마다, 이 깊이의 기저를 두 배로 늘리고 경계+와 경계- 중에서 무작위로 선택한다. 경계+는 p에서 고정 경계를 더한 값을 할당하고 경계-는 q에서 고정 경계를 뺀 값을 할당하는 것이다. 트리의 깊이에 상관없이 경계는 절대 변하지 않는다. 편집 동작을 예측하는 것은 복잡하기 때문에 보상이 손실을 보상할 것이라는 확신을 갖고 트리의 일부 깊이를 희생하는 것이 이 접근방식의 기초가 된다. 

이게 대체 뭔 소리냐?

일부 트리 레벨에서는 비효율적인 전략을 선택할 수 있음. 하지만 이 비효율적 선택이 효율적 선택에 의해 보상될 것임. 각 새로운... 엥?? 몰라. 

 

1) 베이스 더블링

Logoot의 기본 할당 전략은, 식별자를 할당할 때 항상 동일한 베이스를 사용하는 것이다. 트리의 차수(arity)는 베이스 값에 의해 결정된다.

• 베이스 값이 높으면 식별자의 길이가 짧아지지만, 해당 부분에 삽입 연산이 적으면 비효율적일 수 있다.
• 베이스 값이 낮으면 삽입 연산이 많은 부분에서 식별자의 깊이가 깊어져 바운더리 전략의 이점을 충분히 활용하지 못할 수 있다.

따라서 문서의 크기에 따라 베이스의 값을 적응적으로 조정하는 게 좋다. 초기에는 작은 베이스 값으로 시작하고 필요에 따라 베이스 값을 두 배로 늘리는 방식을 제안한다. 이를 통해 문서의 실제 크기를 더 잘 반영할 수 있다. 

 

각 깊이에서 베이스를 두 배로 늘린다는 것은 사용 가능한 식별자 수가 기하급수적으로 증가한다는 뜻이다. 따라서 이 식별자 할당 방식은 지수 트리 모델과 유사하다. 깊이 $k$의 지수 트리는 $N_k=N_{k-1}+k\ast k!$까지 저장할 수 있다.

1. 지수 트리 구조
   • 지수 성장: 트리의 깊이가 깊어질수록, 즉 더 많은 식별자가 필요할수록 사용 가능한 식별자 수가 지수적으로 증가한다.
   • 노드의 자식 수(arity): 트리의 깊이에 따라 각 노드가 가질 수 있는 자식 노드 수가 결정된다. 부모 노드가 가진 자식 노드 수는 그 부모의 깊이에 따라 두 배씩 증가한다. 예를 들어 루트 노드는 베이스 값 만큼의 자식을 가지며 그 자식 노드는 두 배, 그 다음 깊이에서는 다시 두 배로 늘어난다.
2. 식별자의 이진 표현
   • 식별자를 이진법으로 표현할 때, 각 깊이의 식별자는 $b\ast 2^i$(b는 베이스, i는 깊이)로 나타낼 수 있다. 
   • 만약 베이스가 2라면 깊이 1에서는 $2^2$, 깊이 2에서는 $2^3$만큼의 식별자를 선택할 수 있다.
3. 베이스 값 두 배 증가의 전제 조건
   • 공간이 부족하면 식별자의 크기를 늘려야 한다는 전제 하에 베이스 값을 두 배로 증가시키는 방식이다. 
4. 비효율적 할당의 문제점
   • 할당 전략이 비효율적이라면 불필요하게 식별자 크기가 커질 수 있다. 

2) 할당 전략

이전에 바운더리와 랜덤이라는 두 가지 할당 전략을 소개했는데 실험 결과 전자가 후자보다 나은 성능을 보였다. 그러나 바운더리 전략은 애플리케이션에 따라 크게 달라진다. 사용자가 주로 문서 끝에서 삽입 작업을 수행한다면 할당 전략이 효율적으로 수행된다. 그러나 문서 앞쪽에서 삽입 작업을 수행한다면 식별자의 크기를 빠르게 선형적으로 증가시킨다. 

LSEQ에서는 경계-라는 할당 전략을 소개했었다. 기본적으로 이 전략은 원래의 바운더리 전략과 정반대이다. 이 논문에서는 경계+로 이름을 바꾸겠다. 식별자가 p와 q인 두 요소 사이의 삽입 연산을 예로 들어보겠다. 경계+ 전략은 앞의 식별자 p 근처에 식별자를 할당하는 반면, 경계- 전략은 뒤의 식별자 q 근처에 식별자를 할당한다. 

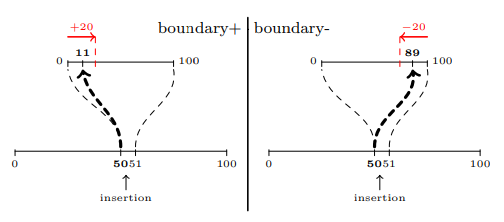
경계+ 알고리즘은 끝 편집을 잘 처리하는 반면, 경계- 알고리즘은 앞 편집을 잘 처리한다. 이 둘은 서로 상반되는 약점을 가지고 있다. 따라서 둘 다 단독으로 안전하게 사용할 수 없다. 

 

3) 할당 전략 선택

모든 시퀀스에 대해 최적의 전략을 구할 수 없기 때문에 LSEQ는 랜덤으로 경계+와 경계-를 번갈아가며 사용한다. 

public class LSEQAllocator {
	private static final int BOUNDARY = 10;
	private Map<Integer, Boolean> S = new HashMap<>();
	private Random random = new Random();
	
	public int[] alloc(int[] p, int[] q) {
		int depth = 0;
		int interval = 0;
		while (interval < 1) {
			depth++;
			interval = prefix(q, depth) - prefix(q, depth) - 1;
		}
		
		int step = Math.min(BOUNDARY, interval);
		
		if (!S.containsKey(depth)) {
			boolean rand = random.nextBoolean();
			S.put(depth, rand);
		}
		
		int id;
		if (S.get(depth)) { // boundary+
			int addVal = random.nextInt(step + 1) + 1;
			id = prefix(p, depth) + addVal;
		} else { // boundary-
			int subVal = random.nextInt(step + 1) + 1;
			id = prefix(q, depth) - subVal;
		}
		
		return convertToArray(id, depth);
	}
	
	private int prefix(int[] id, int depth) {
		int result = 0;
		for (int i = 0; i < depth; i++) {
			if (i < id.length) {
				result += id[i] << (8 * (depth - i - 1));
			} else {
				result += 0;
			}
		}
		return result;
	}
}

위는 할당 함수 LSEQ에 대한 코드이다. 초기 베이스 값은 24, 경계 값은 10으로 설정한다. 선택된 전략을 저장하는 컬렉션 S는 빈 상태로 시작한다. 알고리즘은 세 부분으로 구성된다.

1. 구간 처리
   • 두 식별자 p, q 사이 구간을 처리하여 새 식별자를 할당할 수 있는 범위를 정한다. 이 과정은 깊이마다 진행되며 적어도 하나의 식별자가 삽입될 수 있는 구간을 찾을 때까지 계속된다.
2. 할당 전략 결정
   • 만약 해당 깊이에서 아직 식별자가 할당된 적이 없다면 경계+와 경계- 중에서 랜덤으로 할당 전략을 선택한다. 이 선택은 이후의 결정을 위해 컬렉션 S에 저장된다.
3. 새 식별자 생성
   • 선택된 전략에 따라 이전에 처리된 구간 내에서 랜덤 값을 선택하고 이 값을 p,나 q의 prefix에 추가하거나 빼서 새 식별자를 생성한다.
   • prefix는 주어진 깊이까지의 식별자를 복사하는데 만약 식별자의 크기가 요청된 깊이보다 작으면 부족한 부분을 0으로 채운다.
   • 각 깊이에서 숫자는 해당 깊이의 베이스 값에 따라 인코딩되며, 계산에는 log2(base(cpt)) 비트가 사용된다.

 

4. 실험

1. B : 단순한 경계+ 전략
2. D : 각각의 새 깊이에서의 베이스 더블링 전략
3. RR : 라운드 로빈 전략
4. LSEQ : 베이스 더블링과 랜덤 전략 

1) 경계 B 실험

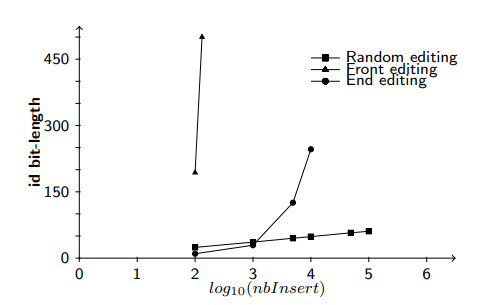
*목표

1. 경계+ 전략이 단조로운 편집 행동(예: 문서가 일정 패턴으로만 편집될 때)이나 삽입 작업 수에 적응하지 않는다는 것을 증명하고자 한다.
2. 단조로운 편집 행동에서는 삽입 작업 수에 비례하여 공간 복잡도가 선형적으로 증가할 것으로 예상된다.
3. 랜덤 편집에서는 식별자 크기가 로그 수준으로 증가할 것으로 예상된다.

*결과

• 요약
  • x축은 로그 스케일로 표시된 삽입 작업 수, y축은 식별자의 평균 비트 길이를 나타낸다.
  • 예상대로 삽입 작업 수가 증가함에 따라 식별자 크기도 증가한다.
• 주요 관찰
  • 랜덤 편집: 식별자 크기 증가가 로그 수준으로 나타났다. 즉, 삽입 작업 수 증가에 따라 식별자 크기가 상대적으로 느리게 증가했다.
  • 앞쪽 및 뒤쪽 편집: 삽입 작업 수에 따라 식별자 크기 증가가 선형으로 나타났다. 특히 앞쪽에서의 편집이 공간 효율성에 부정적이다. 
• 이유
  • 트리의 불균형: 앞쪽, 뒤쪽 편집은 기본적으로 B의 내부 트리 모델을 불균형하게 만든다. 경계+ 전략은 주로 뒤쪽에서의 편집을 처리하도록 설계되었다.
  • 랜덤 편집: 에서는 트리 모델이 균형을 유지하기 때문에 공간 복잡도가 로그 수준으로 나타난다.

 

2) 베이스 더블링 D 실험

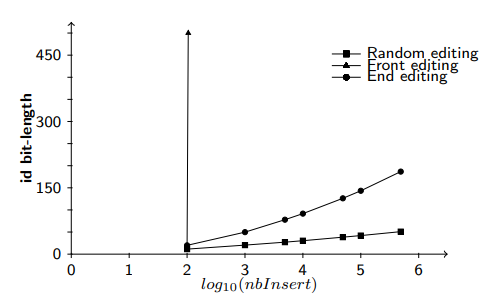
*목표

어떤 경우에도 적합하지 않다는 것을 보여주기 위함이지만, 삽입 횟수 측면에서 확장성이 있기 때문에 B보다 개선된 방식이라고 할 수 있다. 삽입 작업 수에 비례해 식별자 크기가 선형적으로 증가하지 않고 그보다 느리게 증가할 것으로 예상된다. 특히 뒤쪽에서의 편집에서 그렇다. 반면 앞쪽 편집은 B 결과보다 더 나쁜 결과를 보일 것으로 예상된다. 랜덤 편집에서는 로그 형태를 유지할 것으로 기대된다. 

 

*결과

• 요약
  • B 처럼 D에서도 삽입 작업 수 증가함에 따라 식별자 크기가 계속 증가한다.
• 주요 관찰
  • 예상된 편집 패턴(뒤쪽)에서는 식별자 크기 증가가 상대적으로 느리다.
  • 반면 예상치 못한 편집 패턴(앞쪽)에서는 식별자 크기가 이차적(quadratic)으로 증가한다. 더 빠르게 증가한다는 뜻.
• 이유
  • 베이스 더블링은 이전 레벨에서 트리 생성을 촉발했다는 가정에 기반한다. 이를 통해 새 레벨에서 사용 가능한 식별자 수가 늘어난다.
  • 만약 이전 레벨들이 삽입 작업으로 포화 상태에 있었다면 이 가정이 확인되어 효율적인 할당이 이뤄지지만, 이 가정이 틀리면 각 새 레벨은 단 하나의 식별자만 포함하게 될 수도 있다. 

 

3) 라운드 로빈 전략

 

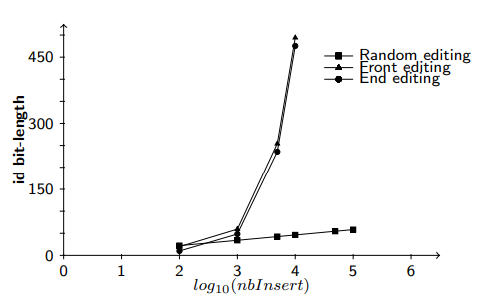
*결과

• 요약
  • 특정 최악의 경우를 피하면서도 많은 삽입 작업에 효율적으로 적응하지 못한다. 
• 주요 관찰
  • 랜덤 편집: 식별자 크기 곡선이 로그 형태를 유지한다. 상대적으로 느리게 증가.
  • 앞쪽 및 뒤쪽 편집: 모두 식별자 크기 증가가 선형적이다.
• 이유
  • B와 비교하여 뒤쪽 편집에서 식별자의 평균 비트 길이가 두 배 빠르게 증가한다. 이는 RR 전략이 교대로 할당 전략을 변경하여 앞쪽에서의 최악의 경우를 피하기 때문이다.
  • 위의 이유로 인해 전체 시간의 절반 동안 적절한 전략을 사용하지 않으므로 식별자 크기 증가율이 두 배로 나타나는 것이다. 
  • RR 전략은 한 레벨의 손실을 다음 레벨에서 얻은 이익으로 상쇄하지 못한다. 전체적인 공간 효율성 개선에 한계가 있다. 

4) LSEQ 전략

 

*목표

편집 동작 의존성 문제와 삽입 작업 수에 대한 비적응성 문제를 모두 해결한다는 것을 보여주는 것이 목표이다. 흑흑

 

*설명

 

*결과

• 요약
  • 평균 비트 길이 값은 D 전략와 유사하다. 이는 LSEQ가 일부 깊이를 잃었지만 미래의 삽입 작업들이 그 손실을 빠르게 상쇄한다는 것을 의미한다. 
• 주요 관찰
  • 앞쪽 및 뒤쪽 편집: 식별자 크기 증가가 삽입 작업 수에 비해 상대적으로 느리다.
  • 랜덤 편집: 다항-로그형으로 나타난다. 매우 느리게 식별자 크기 증가한다는 뜻.
• 이유
  • 베이스 더블링은 특정 가정(삽입 작업 수가 맣아짐에 따라 새 레벨 생성된다는 가정)이 맞을 때 효과적이다. 이 가정이 참일 때 추가적인 삽입 작업에 대비해 충분한 식별자 공간을 확보할 수 있다.
  • 경계+, 경계- 전략을 무작위로 선택하는데 이 선택이 베이스 더블링 가정을 성립시키는 확률을 50%로 유지한다.
  • 잃어버린 이전 레벨의 손실을 보상할 만큼 충분한 이득을 얻기 때문에 전체적으로 서브-선형적 공간 복잡도를 갖는다. 

 

5. 나의 이해하려는 노력

이전 레벨 손실의 의미

LSEQ 전략은 삽입 작업이 많아지면 베이스를 두 배로 증가시켜 더 많은 식별자 공간을 확보한다. 하지만 새 레벨(깊이)이 생성되었을 때 해당 레벨에 할당할 수 있는 식별자 공간이 모두 사용되지 않을 수도 있다. 비어있는 상태로 남을 수 있다는 뜻이다. 이게 잃어버린 레벨이라는 뜻. 

내 생각을 덧붙이면, 삽입 작업 수가 꾸준히 증가할 것이라는 가정 하에 손실이 상쇄된다고 주장하는 것 같다. 초반에는 할당한 식별자 공간이 모두 활용되지 못할 수도 있지만, 계속해서 삽입 작업이 증가하면 할수록 확보한 식별자 공간이 사용될 것이고 이에 따라 상쇄된다고 하는 듯. 

 

LSEQ에서 베이스 더블링과 달리 앞쪽 편집에서 공간 복잡도가 로그인 이유

근데 LSEQ에서 베이스 더블링과 달리 앞쪽 편집에서 공간 복잡도가 로그인 이유를 모르겠다. 왜지? 

그러니까, 베이스 더블링 가정을 이전 레벨에서 트리 생성을 촉발했다는 가정이라고 하자. 즉, 예를 들어 레벨 1에서 2개의 식별자 공간이 모두 사용되어 새 삽입 연산을 수행할 공간이 없기 때문에 레벨 2가 생성되었다는 뜻이다. 

내가 이해하기로는, 베이스 더블링 전략(D)에서는 새 레벨을 만들어도 그 레벨이서 사용 가능한 식별자 수가 충분하지 않아서 계속 레벨을 만들고, 레벨이 너무 깊어지니까 그에 따라 식별자 크기가 빠르게 증가하는데, 즉 베이스 더블링 가정이 계속해서 틀리는 것인데. 그에 반해 LSEQ 전략에서는 경계+, 경계- 전략을 무작위로 선택해서 베이스 더블링 가정의 성립 확률을 50%로 유지하는 것이다.